Skaláry a vektory
Operácie s vektormi
Opačný vektor
Rovnaké vektory
Súčet vektorov
Rozdiel vektorov
Súčin vektora a skalára
Skalárny súčin
Vektorový súčin
Rozklad vektora na zložky
Diferenciálne
a integrálne operácie s vektormi
Skaláry a vektory
Vo fyzike sa najčastejšie stretávame s fyzikálnymi veličinami, ktoré môžeme
rozdeliť na skaláry a vektory.
Skalár je fyzikálna veličina, ktorá je úplne určená svojou veľkosťou,
t.j. číselnou hodnotou v príslušných jednotkách. K týmto veličinám patrí
napr. dĺžka, hmotnosť, čas, teplota, energia, elektrický náboj a iné.
Príklady: m = 50 kg, E = 2 J,
t = 200 C
Vektor je taká fyzikálna veličina, ktorá je určená svojou veľkosťou
a smerom. Príkladom vektorových veličín môže byť rýchlosť, hybnosť,
sila, moment sily, intenzita elektrického poľa a ďalšie.
Príklady: sila, moment sily, rýchlosť:
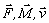
Pre označenie vektorov sa používajú písmená so šípkami alebo vodorovnými
čiarkami alebo tučné písmená v tlačenom texte (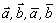 , a, b).
, a, b).
Graficky sa vektory označujú orientovanými úsečkami, pričom dĺžka
úsečky vyjadruje veľkosť vektora a šípka určuje jeho smer (Obr. 1).

Obr. 1: Smer vektora udáva šípka a dĺžka úsečky
jeho veľkosť.
Každý vektor môžeme vyjadriť súčinom veľkosti daného vektora a
jednotkového vektora, ktorého smer je totožný so smerom daného vektora. Veľkosť
jednotkového vektora sa rovná +1. Teda pre vektor
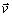 môžeme písať
môžeme písať
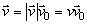
kde
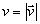 je veľkosť
vektora
je veľkosť
vektora
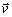 a
a
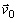 je jeho jednotkový vektor (Obr. 2).
je jeho jednotkový vektor (Obr. 2).

Obr. 2: Vektor
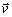 a
jeho jednotkový vektor
a
jeho jednotkový vektor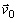 .
.
Operácie s vektormi
Pri počítaní so skalármi a vektormi sa často stretávame s operátormi,
ktoré značne zjednodušujú výpočty. Operátorom rozumieme znak alebo súbor
znakov, ktoré definujú určitú operáciu s príslušnou funkciou.
Opačný vektor
Vektor
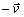 má
rovnakú veľkosť, ale opačný smer ako vektor
má
rovnakú veľkosť, ale opačný smer ako vektor
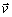 .
.

Obr. 3: Opačný vektor ku vektoru
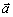 .
.
Rovnaké vektory
Dva vektory
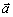 a
a
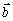 považujeme za totožné,
keď majú rovnaké veľkosti aj rovnaké smery.
považujeme za totožné,
keď majú rovnaké veľkosti aj rovnaké smery.
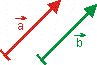
Obr. 4: Rovnaké vektory.
Súčet vektorov
Súčet dvoch
vektorov
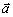 a
a
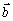 je vektor
je vektor
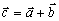 , ktorý
dostaneme, keď ku koncovému bodu vektora
, ktorý
dostaneme, keď ku koncovému bodu vektora 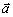 pridáme vektor
pridáme vektor 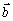 (Obr. 5a). Vektor
(Obr. 5a). Vektor
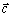 je určený začiatočnými bodom vektora
je určený začiatočnými bodom vektora
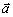 a koncovým bodom vektora
a koncovým bodom vektora
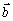 .
.
Vektor 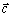 dostaneme aj pomocou rovnobežníka zostrojeného
z vektorov
dostaneme aj pomocou rovnobežníka zostrojeného
z vektorov 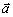 a
a
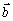 .
Vektor
.
Vektor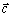 je potom určený uhlopriečkou
rovnobežníka (Obr. 5b).
je potom určený uhlopriečkou
rovnobežníka (Obr. 5b).
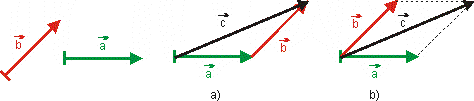
Obr. 5: Súčet vektorov.
Pre súčet dvoch vektorov platí komutatívny zákon
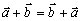
Rozdiel vektorov
Rozdiel dvoch vektorov 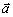 a
a 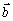 je vektor
je vektor
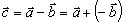 , ktorý
určíme podľa pravidla pre sčítanie dvoch vektorov tak, že ku vektoru
, ktorý
určíme podľa pravidla pre sčítanie dvoch vektorov tak, že ku vektoru 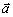 pripočítame vektor
pripočítame vektor
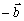 .
.
Súčin vektora a skalára
Súčinom skalárnej veličiny s a vektora 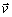 dostaneme vektor
dostaneme vektor
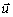 , pre
ktorý platí
, pre
ktorý platí
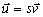 .
.
pričom ak s > 0, vektor 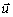 má rovnaký smer
ako
má rovnaký smer
ako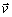 , a ak
s < 0, vektor
, a ak
s < 0, vektor
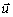 má opačný smer než
má opačný smer než 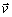 . Pre veľkosť vektora
. Pre veľkosť vektora
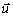 platí
platí
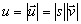 .
.
Skalárny súčin
Skalárny súčin dvoch vektorov 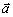 a
a 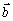 , ktorý sa označuje
, ktorý sa označuje
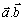 je definovaný vzťahom
je definovaný vzťahom
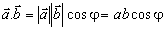
v ktorom
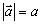 a
a
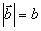 sú veľkosti
príslušných vektorov a j je uhol, ktorý zvierajú
vektory
sú veľkosti
príslušných vektorov a j je uhol, ktorý zvierajú
vektory 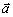 a
a
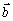 . Výsledkom skalárneho násobenia je skalár.
. Výsledkom skalárneho násobenia je skalár.
Špeciálne prípady:
1. keď vektor 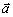 je rovnobežný
s vektorom
je rovnobežný
s vektorom 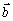 skalárny súčin
skalárny súčin
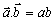 (1) (Obr. 6a),
(1) (Obr. 6a),
2. ak vektor 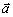 je kolmý na
vektor
je kolmý na
vektor 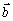 , potom
, potom
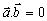 (2) (Obr. 6b).
(2) (Obr. 6b).
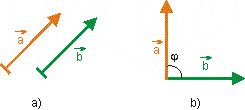
Obr. 6: Špeciálne prípady skalárneho súčinu dvoch
vektorov.
 |
Vo
vzťahu (1) cos j = 1,
pretože j = 00
pre skalárny súčin a vo vzťahu (2) cos
j = 0, pretože j = 900. |
Pre skalárny súčin platí
komutatívny zákon
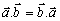
distributívny zákon
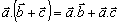
Vektorový súčin
Vektorovým násobením vektora 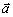 s vektorom
s vektorom
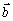 , ktorý sa označuje
, ktorý sa označuje
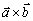 dostaneme vektor
dostaneme vektor
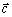 , ktorého veľkosť
, ktorého veľkosť
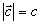
je definovaná vzťahom
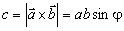 .
.
Vektor
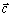 leží v priamke, ktorá je kolmá na rovinu určenú vektormi
leží v priamke, ktorá je kolmá na rovinu určenú vektormi 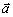 a
a 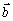 a smeruje na tú stranu uvažovanej roviny, z ktorej
stotožnenie prvého vektora (
a smeruje na tú stranu uvažovanej roviny, z ktorej
stotožnenie prvého vektora (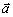 ) s druhým
(
) s druhým
(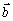 ) na kratšej
ceste sa javí proti smeru hodinových ručičiek (obr.7).
) na kratšej
ceste sa javí proti smeru hodinových ručičiek (obr.7).
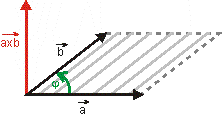
Obr. 7: Výsledný vektor vektorového súčinu leží na
priamke kolmej na rovinu určenú vektormi a a b, v tomto prípade
smeruje nahor.
Špeciálne prípady:
1. ak vektory 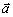 a
a 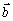 sú
rovnobežné, potom
sú
rovnobežné, potom 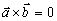 (3),
(3),
2. ak vektory 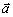 a
a 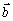 sú navzájom
kolmé, potom veľkosť vektora
sú navzájom
kolmé, potom veľkosť vektora
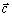 je
je
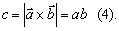
Pre vektorový súčin
neplatí komutatívny zákon, možno však písať
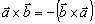
platí distributívny zákon
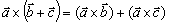
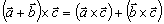
 |
Vo
vzťahu (3) sin j = 0,
pretože j = 00 pre
vektorový súčin a vo vzťahu (4) cos
j = 1, pretože j = 900. |
Ďalšie zdroje:
http://www.kf.elf.stuba.sk/~cerven
v časti domáce animácie si pozrite Rýchlokurz vektorov