Matematicko - fyzikálne tabuľky Derivácie     6/7

Predchádzajúca strana

Úvod

Ďalšia strana

 

Derivácia
Derivácia v matematike
Derivácie základných funkcií
Vety o deriváciách
Druhá derivácia
Geometrický význam derivácie
Derivácia vo fyzike

 

Derivácia
Pojem derivácie patrí do základov matematickej analýzy. Ako ,,pracovný nástroj" ho začal používať I. Newton pri riešení fyzikálnych úloh a G. W. Leibniz pri riešení geometrických úloh. Považujeme ich za nezávislých objaviteľov infinitenzimálneho počtu. Táto oblasť bola rozvíjaná mnohými matematikmi, ktorí prispeli originálnymi výsledkami, ale prelom medzi týmito výsledkami a zdôvodnením základov analýzy začal český matematik B. Bolzano a A. L. Cauchy, keď deriváciu definoval pomocou limity.

 

Derivácia v matematike
Definícia derivácie: Nech je daná funkcia f(x) a bod. Funkcia f(x) má deriváciu v bode x0, ak existuje limita podielu
.   (1a)

Túto limitu označujeme znakom alebo (označenie podľa Lagrangea) a nazývame ju deriváciou funkcie v bode x0: .  (1b)

Ak má funkcia v bode x0 deriváciu hovoríme, že je v bode x0 diferencovateľná.

 

Ak pre funkciu použijeme označenie y = f(x), niekedy jej deriváciu v čísle x0 označujeme y´(x0).V matematike sa častejšie používa Lagrangeovo označenie derivácie , ale existuje aj označenie derivácie podľa Leibniza (používa sa viac vo fyzike)   v tvare  resp.  (2).

 

 

Derivácie základných funkcií

funkcia jej derivácia v bode podmienky
 
    x > 0
 y´ = 0  











 
a>0


    x > 0
, a > 0

    x > 0



Vety o deriváciách
Ak funkcie f(x), g(x) majú v bode x0 deriváciu, tak má v bode x0 deriváciu aj:
1. funkcia f(x).g(x) a platí: (f(x0).g(x0))´ = f ´(x0).g(x0) + f(x0).g´(x0),
2. funkcia c.f(x),a platí: (c.f(x0))´ = c.f ´(x0),
3. funkcia f(x) + g(x) a platí: (f(x0) + g(x0))´ = f ´(x0) + g´(x0),
4. funkcia , ak : .


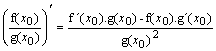5.derivácia zloženej funkcie:
Nech funkcia g má deriváciu  v bode a funkcia f nech má deriváciu v bode. Potom zložená funkcia y = f(g(x)) má deriváciu v bode x0 a platí: .

 

Druhá derivácia
Nech funkcia f je diferencovateľná na , t.j. existuje funkcia f ´. Ak je táto funkcia diferencovateľná v bode , nazývame jej deriváciu druhou deriváciou f v bode x0.
Zápis: f ´´(x0),  y´´(x0), f(2)(x0), .

 

Geometrický význam derivácie
Derivácia funkcie f(x) v bode x0 je rovná smernici dotyčnice vedenej k čiare f(x) jej bodom [x0, f(x0)]: k = f ´(x0). Potom rovnica dotyčnice ku grafu funkcie v dotykovom bode má tvar:  f(x) - f(x0) = k(x - x0), kde k = tg j. Úpravou pre definíciu derivácie f(x) v bode x0
  .

 

Derivácia vo fyzike
 Vo fyzike sa používa prvá aj druhá derivácia, pri výpočte sa aplikujú tie isté matematické vzťahy pre derivovanie. Pre označenie týchto derivácii sa používa Leibnizov zápis (2) pre prvú deriváciu:


kde f je funkcia, ktorú derivujeme, x je premenná, podľa ktorej derivujeme.

Zápis druhej derivácie:
.
    

Pozor výraz nepredstavuje podiel a číslo 2 nepredstavuje druhú mocninu, ale naznačuje druhú deriváciu vo výraze .


Príklad 1:
Zápis  

predstavuje prvú deriváciu rýchlosti podľa času, v(t) je funkcia rýchlosti, ktorá je derivovaná podľa premennej t.

Napríklad funkcia rýchlosti je v(t) =kt, jej derivácia je .

Príklad 2:
Zápis  

predstavuje druhú deriváciu dráhy podľa času, s(t) je funkcia dráhy, ktorá sa dvakrát derivuje podľa času t.  

Napríklad funkcia dráhy je daná s(t) = 3t2, prvá derivácia , druhá derivácia .