Fractional calculus in control theory
Key words: fractional
calculus, control
theory, fractional-order controlled system, fractional-order
controller.
1. Introduction
The use of fractional calculus for modelling physical systems has been
considered (Oldham et al., 1974; Torvik et al., 1984; Westerlund et al.,
1994). We can find also works dealing with the application of this mathematical
tool in control theory (Axtell et al., 1990; Dorcak, 1994; Outstaloup,
1995; Podlubny, 1994). We can use this mathematical tool for description
of the controlled object and also for a new type of controller: fractional-order
controller. Motivation on using the fractional-order controllers was that
PID controllers belong to the dominating industrial controllers and therefore
there is a continuous effort to improve their quality and robustness. One
of the possibilities to improve PID controllers is to use fractional-order
PID controllers with non-integer differentiation and integration parts.
2. Fractional-order controlled system
The fractional-order controlled system can be described by the fractional-order
model with the continuous transfer function in the form:
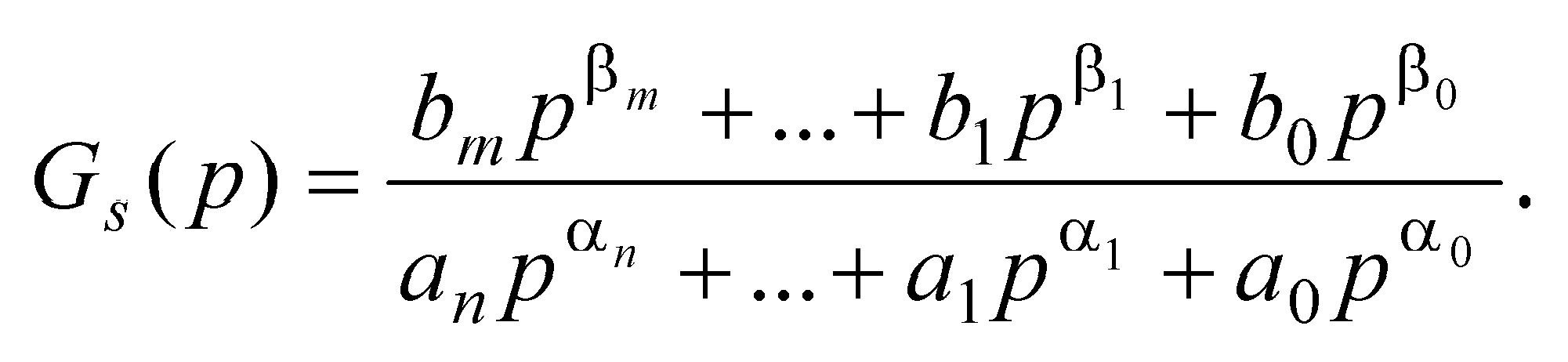
3. Fractional-order controller
The fractional-order controller can be described by the fractional-order
continuous transfer function
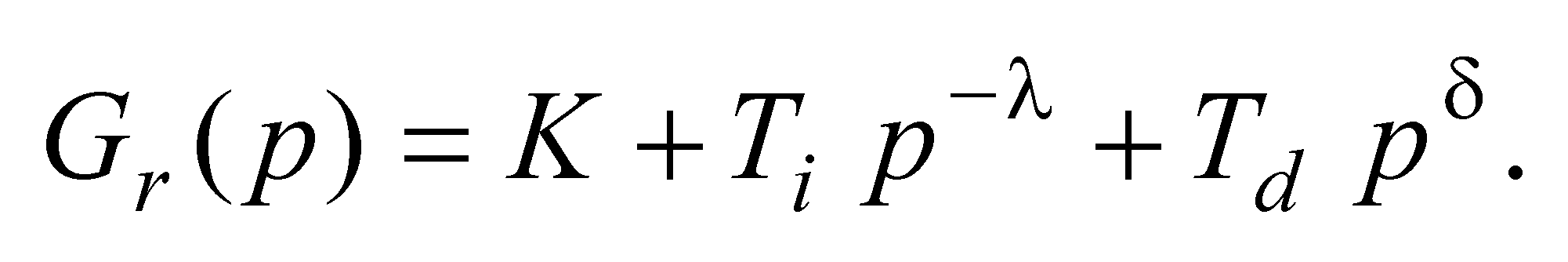
where lambda is an integral order, delta is a derivation
order, K is a proportional constant, Ti is an integration
constant and Td is a derivation constant.
4. Main research topics in control theory
Fractional calculus in control theory is a new area of research. The
most important topics are:
-
controller parameters design methods,
-
control algorithm,
-
digital and analogue realization of fractional-order controllers,
-
identification methods,
-
modelling and simulation of control systems,
-
stability.
References
-
Axtell, M. and Bise, M. E. Fractional Calculus Applications in Control
Systems. IEEE 1990 National Aerospace and Electronics Conference,
New York, 1990, pp. 563 - 566.
-
Dorcak, L. Numerical Models for Simulation of the Fractional-Order Control
Systems. UEF - 04 - 94, Slovak Academy of Science, Institute of
Experimental Physics, Kosice, 1994.
-
Gorenflo, R.Fractional Calculus: Some Numerical Methods: Fractals and
Fractional Calculus in Continuum Mechanics. CISM Lecture Notes,
Springer Verlag, Wien, 1997, pp. 277 - 290.
-
Lubich, Ch. Discretized fractional calculus. SIAM J. Math. Anal.,
vol. 17, no. 3, 1986, pp. 704 - 719.
-
Oldham, K. B. and Spanier, J. The Fractional Calculus. Academic
Press, New York, 1974.
-
Oustaloup, A. La Derivation non Entiere. Hermes, Paris,1995.
-
Petras, I. List of publications.
-
Podlubny, I.. Fractional - Order Systems and Fractional - Order Controllers.
UEF - 03 - 94, Slovak Academy of Sciences, Institute of Experimental
Physics, Kosice, 1994.
-
Torvik, P. J. and Bagley, R. L.. On the appearance of the fractional
derivative in behaviour of real materials, Trans. of the ASME, vol.
51, 1984, pp. 294 - 298.
-
Westerlund, S. and Ekstam, L. Capacitor theory. IEEE Trans. on
Dielectrics and Electrical Insulation, vol. 1, no. 5, 1994, pp. 826 - 839.
[Back to previous page]
This Web site was created by Ivo Petras. All rights reserved.
Copyright © 2002, 2003.
Last updated:
Jan. 31, 2003.
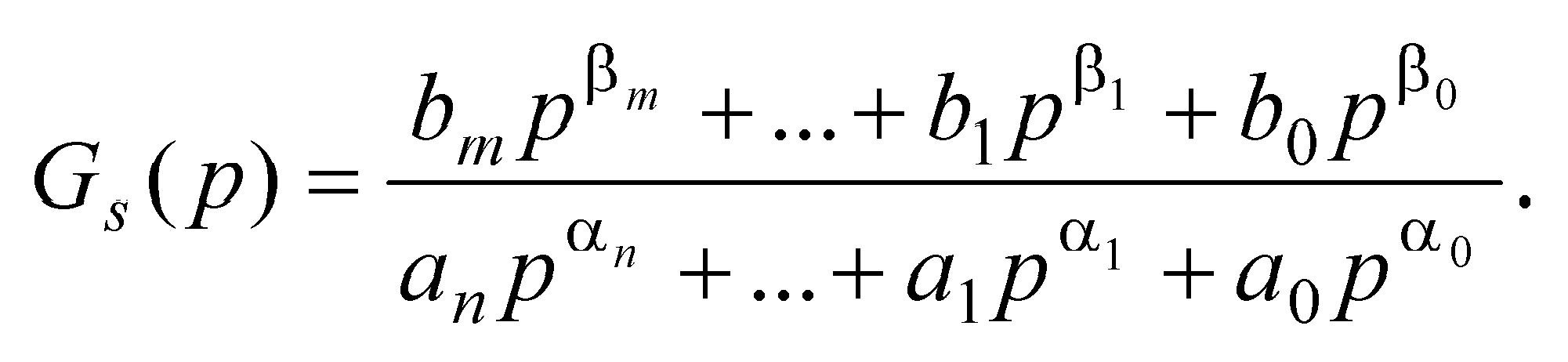
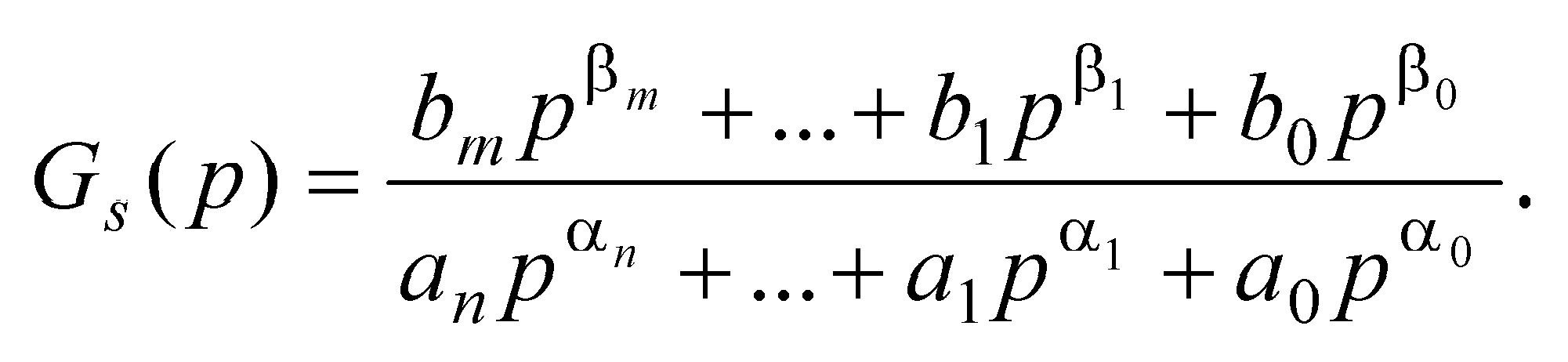
![]()